
[统计学]什么是无偏估计?为何方差的无偏估计要/n-1?
我自己从事品质方面的工作,除了解决工作上的实际问题积累实战经验之外,工作之余也顺便考了日本品质管理检定。资格级别越高要求量化分析能力越强,当时的难点就是假设检验。而想搞懂假设检验,无偏估计必须理解。
这篇文章主要解释下列问题。
・方差与方差的无偏估计有何不同
・为什么方差的无偏估计的除数为(n-1)
总体是指想要调查的所有对象,样本是指想要调查的所有对象的其中一部分。
你们学校非常人性化,考试不公布学生的成绩和排名。期末考完了,你想知道自己到底在班中啥水平,于是你牺牲了几个课间休息时间,去问每个人的成绩。后来同学看出你的目的,就告诉了你假成绩,你擦干满头大汉,计算器一顿猛敲,一算,妥妥的,自己分数碾压平均分,你喜上眉梢,周围同学也都对你表示祝贺。
后来要高考了,根据以往经验,你知道学校前10%左右会考上重点大学,于是你在考完摸底考试后,想要看看自己在整个年级大约处于啥水平。但是去问每个人不现实,自己班还可以厚着脸皮问一下,别的班的认识的人很少,于是,你问度娘,发现了这个博客,得知可以用抽样调查的方法,于是你兴冲冲的去调查,结果发现自己远远低于平均分。。。
这个栗子中,你调查总体会有几个大问题:
1.需要花费大量时间和精力
2.很难保证所有数据都是真实的
3.有时无法得到所有数据
要是能问一些人就知道整个年级的平均值,那就太好了。宇宙最强学科统计学告诉你是可以的。
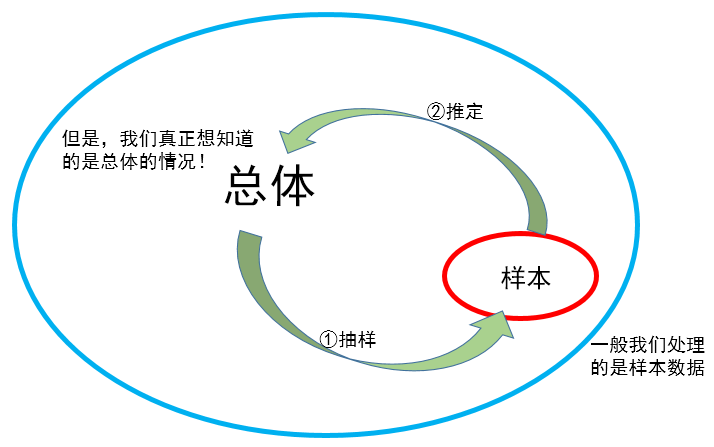
必须先明确你的目的是总体,不过因为很多原因你没法直接研究,只能通过样本来反推总体!
接下来,需要知道总体和样本的关系。
总体的性质和从总体中的抽取的样本的性质不一定相同!
总体的平均值,方差,标准差和样本的平均值,方差,标准差不一定相同。这句话很重要,自己心里默念3遍。所以统计学中总体和样本的统计值是区别开的。为了继续解释,现在明确几个基本概念。
期望(均值)
是指随机事件中随机变量和它出现概率的乘积的总和,反映了随机变量平均取值的大小。
方差
是用来度量随机变量和其均值之间的偏离程度,方差越小,偏离程度越小。
- 样本方差:一般讲的方差,样本的离散程度,除数为n;
- 总体方差:这个值往往由于客观原因如成本,时间,技术手段等无法得到,是我们想知道的。
- 总体方差的无偏估计:用样本来估计总体时用的方差,总体的离散程度,除数为(n-1);
统计量
已知样本集,由样本值计算的函数,被称为统计量,不含未知参数。比如样本平均值,样本方差,样本标准差等。
估计量
设总体样本的分布函数已知,参数未知。已知样本集,需要构造适当的统计量来估计未知参数的近似值,这被称为估计量。
目的不要忘了,就是用统计量估计总体。

至此回答了第一个问题:
- 方差与方差的无偏估计有何不同
第二个问题:
- 为什么方差的无偏估计的除数为(n-1)
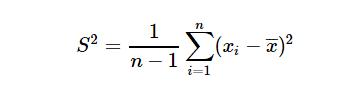
我知道同年级50个同学的考试分数,想要推断年级所有人的方差的时候,你会发现这第50个值确定的一瞬间,客观上第50个值的均值也定下了,就算你拿掉50个值中的任何一个,因为49个值和均值已知,你都可以算出第50个值,相当于自由度其实只有49。
为了加深理解再举个栗子,买彩票,猜7个数字。因为重大使命,我从未来穿越到你面前,告诉你下期会开奖的数字,由于我没有RMB,我跟你商量你帮我买然后咱俩分钱。奖金是1个小目标,有两个方案:
①我告诉你7个数字,我拿9成奖金;
②我只告诉你6个数字和7个数字的均值,我拿1成奖金。
你会选哪个方案?为什么?
除数为(n-1)数学上的证明可以看教科书,不写进来了。直观上理解了,才能更好地应用到实际中。