1.1 学習目的
- 基本概念
- ワイブル解析の役割
- ワイブル分布の特徴
- 改善を定量化する方法
- 信頼性を予測する方法
- 信頼性試験を効率よく実施する方法
- 潜在故障を未然に防止する方法
1.2 適用事例
- ある中古車のバイヤーは、100,000Km走行したあるモデルでトランスミッションの故障が発生する確率を知りたい
- ある製品サポ-トエンジニアは、現在発生している問題がどのような故障パタ-ンであるか知りたい
- 開発品の寿命試験の結果から、信頼性に関する保証レベルを判断したい
2.1 信頼性とは
JIS-Z8115:2000『信頼性用語 (Glossary of Terms Used in Reliablity)』において、「アイテムが与えられた条件で規定の期間中、要求された機能を果たすことができる性質」と定義される。
2.2 信頼性の三要素
耐久性、保全性、人間・設計信頼性
2.3 用語の解説
・非修理系 : 故障したときに修理しないで廃棄してしまうもの
・平均故障率 : λ=故障数/動作時間(1/h:時間)
・MTTF : 平均故障寿命(mean time to failure)
MTTF = 動作時間/故障数
・修理系 : 故障したときに修理や部品の交換により、再び使用し続けることができるもの
・MTBF : 平均故障動作時間(mean time operating time between failures)
MTBF = 動作時間/故障数(h:時間)
・B10ライン : 全体の10(%)が故障するまでの時間をB10ライフと呼ぶ
・R(t) : 信頼度(Reliability)【時間tでの残存確率】
・F(t) : 不信頼度(Failure)【時間tでの故障確率】
・MTTR : 平均修復時間(mean time to repair)
・稼働率 = MTBF/(MTBF+MTTR)
*注意: 平均故障率とMTBFについて、偶発故障のときのみ計算できる。初期故障と摩耗故障のときは計算できない
・バスタブ曲線 : バスタブ曲線(bathtub curve)は、機械や装置が運用され始めてから、やがて寿命を迎えるまでの期間を、「初期故障期」「偶発故障期」「摩耗故障期」の3つに区分し、横軸に経過時間tを、縦軸に故障率をとるグラフ(Fig1)
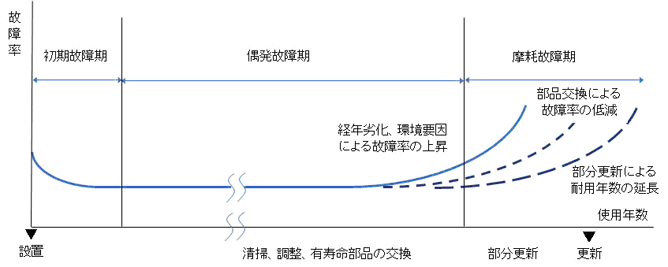
Fig1 バスタブ曲線
3.1 信頼度
信頼度はアイテムが与えられた条件下で与えられた時間隔(t1 t2)に対して要求機能を実行できる確率(JISZ8115:2000)に定義されている。
通常は(0,T)間の信頼度を考え、それをR(t)で表す。
1. 確率密度関数f(t)と時間軸で囲まれた時間Tにより右側の面積に相当する
2. 信頼度は時間の関数であり、1からゼロに向かう単調減少の関数となる
3. 確率密度関数はデータ数が多ければ、ヒストグラムで近似することができる
不信頼度F(t)は時間tまでに故障したものの累積故障割合を表し、信頼度関数R(t)とは全てのt≥0で信頼度十不信頼度=R(t)+F(t)=1の関係にある。Fig2
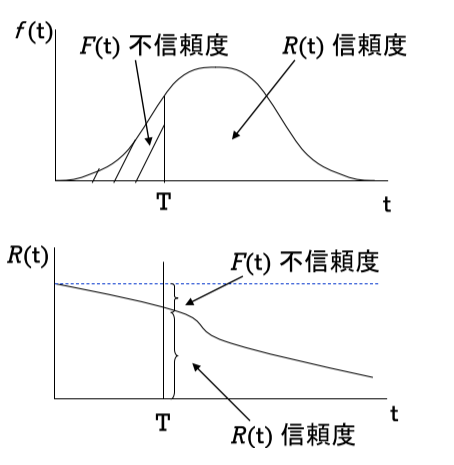
Fig2 f(t)確率密度関数 R(t)信頼度関数
確率密度関数は、データが多いとヒストグラムで近似することができる。Fig3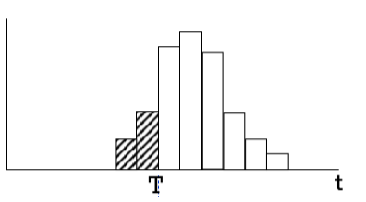
Fig3 ヒストグラム
サンプルの故障時間を表すグラフFig4、×故障 ○正常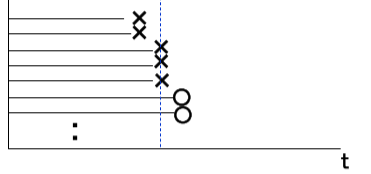
Fig4 信頼度寿命データ
3.2 MTTF
MTTF :平均故障寿命(mean time to failure)
MTTF = 動作時間/故障数
例:5つの部品のサンプルを信頼性試験を行なった結果から下のFig5に示す寿命データが得られた。このデータから200時間における信頼度R(200)とMTTFを求める。
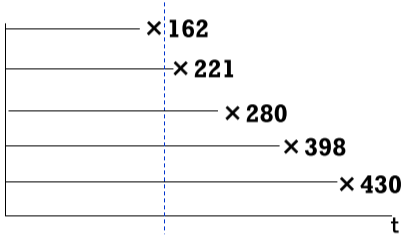
Fig5 寿命データ
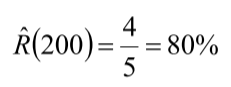
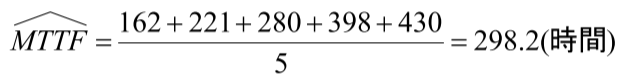
つづく