[统计学]什么是正态分布?图解来说清楚
目录
0.正态分布是学习统计学的基础
1.正态分布是什么样的?
2.正态分布的性质
3.用Excel画正态分布
4.总结
0.正态分布是学习统计学的基础
想学正态分布,发现书上一堆公式和推导,小心脏凉了一半。。。就没有然后了。我也被书本教过做人,所以想尽可能简单的说明白正态分布,且让人有继续学下去的动力。
正态分布广泛的运用在统计检验,统计推定等各个统计学应用中。说到正态分布,可能脑海中首先浮现的是一个山型的曲线。没错,正态分布就是学习统计学的一座大山,不过爬过去后发现其实不过是一个小山头,不要担心,因为后面有更高的大山在等着你!
1.正态分布是什么样的?
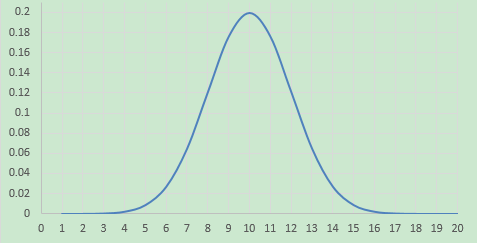
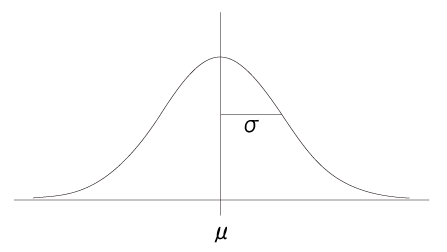
正态分布(又称高斯分布)的形状如下图。因为形状看起来像一个钟,所有描绘正态分布的曲线又称为钟形曲线。
|

|
横轴是观测数据,纵轴是观测值对应的发生概率(概率密度)
正态分布有这几个特征:
①左右对称
②均值的发生概率最大,
③离平均越远,发生的概率越小,
为什么在统计学中正态分布如何重要?
因为自然界和人类社会中,符合正态分布的事物实在太多了。
原因是“不论总体是什么分布,只要从总体抽出的样本数足够多的时候,样本平均的分布符合正态分布。”这个性质称为中心极限定理。关于中心极限定理请参考→[统计学]什么是中心极限定理?一文搞懂中心极限定理
也是因为存在这个性质,很多的统计方法都假设数据是符合正态分布的。
2.正态分布的性质
正态分布有两条非常重要的性质。
1.正态分布的形状是平均和标准差(数据离散程度)决定的。
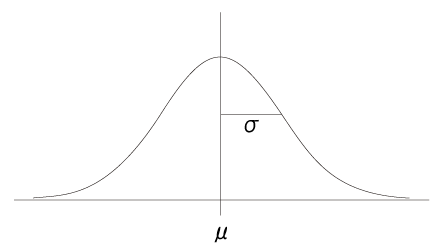
平均μ决定了正态分布的中心位置。
标准差σ决定了正态分布左右展开的幅度大小。
正态分布的表达式如下。
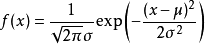
2.知道标准差后,范围内有多少观测数据也就知道了。 知道标准差后,范围内有多少观测数据也就知道了。
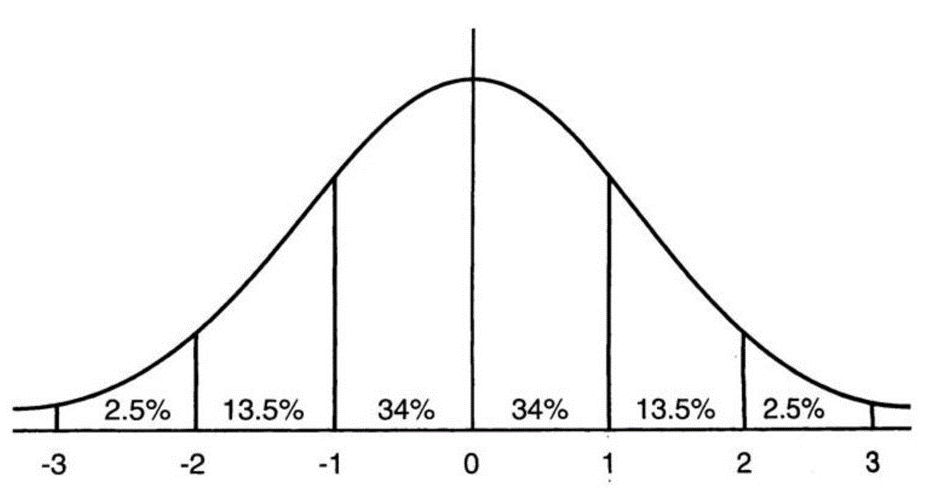
这条性质跟正态分布的平均和标准差的值无关。
所以知道标准差后,范围内有多少观测数据也就知道了。
举个品质管理方面SPC控制图的例子:
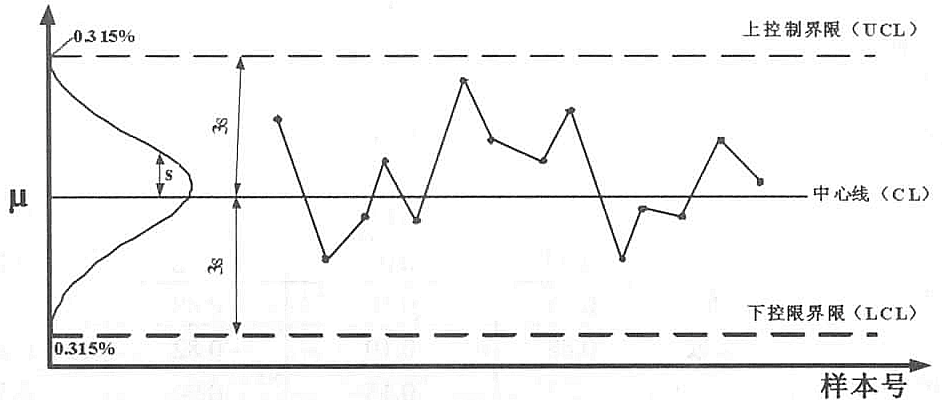
你们公司生产吸管,规定长度μ为100mm。你拿游标卡尺抽样测量吸管长度,虽然你不能预测每一次的测量结果,但是慢慢你会发现大多数测量结果都在100mm附近,离100mm越远,测量结果的次数越少。
3.用Excel画正态分布
光说不练假把式,看懂了和自己能动手做完全不是一回事,看了就觉得自己懂了属于人生三大错觉之一。有兴趣可以去搜一下这属于第几大错觉。
所以接下来打开你电脑上的Excel,动手画一下。
- 使用NORM.DIST函数画钟形曲线
因为日语版操作系统,菜单提示都是日语,不要在意。看菜单的位置和图标就可以。
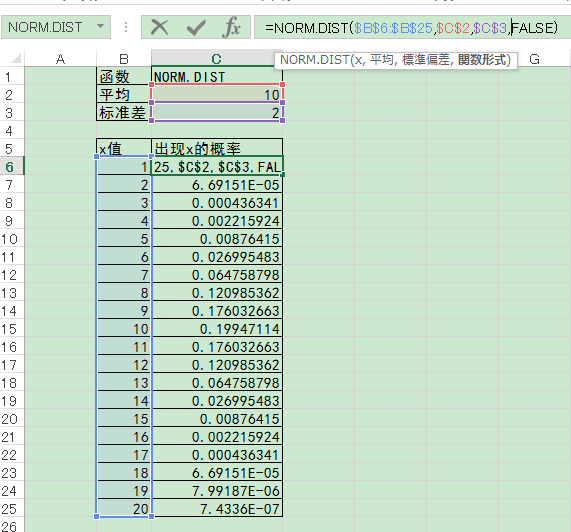
NORM.DIST函数有4个参数,x值,平均,标准差,及函数形式。
函数形式输入FALSE,其余三个参数根据下图进行选择。x为1~20,平均为10,标准差为2。
①求x为1~20时的概率。
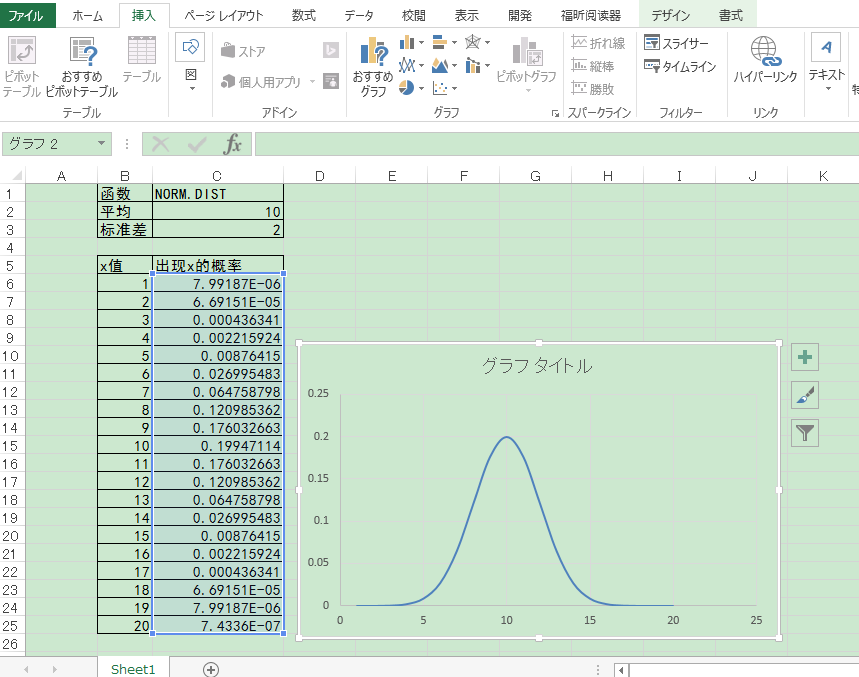
②选择散步图中的平滑线。
③画出平均为10,标准差为2的正态分布曲线。
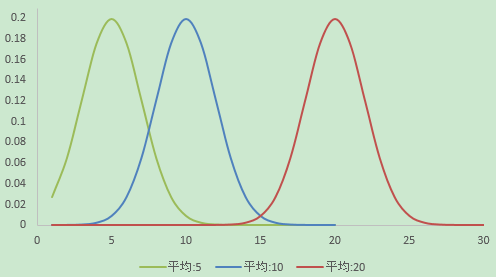
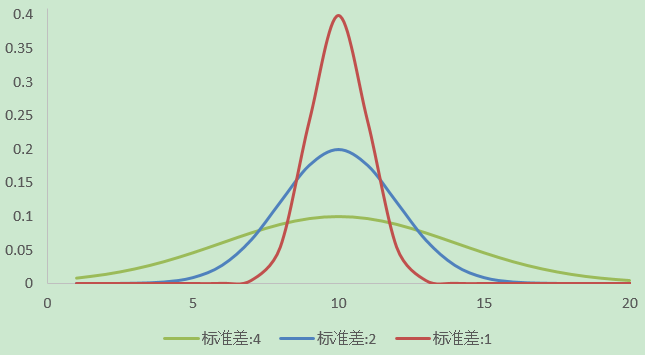
接下来我们让标准差不变,改变平均,看看曲线的变化情况。
- 平均决定了正态分布的中心位置。
发现平均越大,正态分布曲线右移;同时平均越小,正态分布曲线左移。
标准差不变,正态分布曲线的形状不变,所以正态分布曲线的形状与平均无关。
接下来平均不变,改变标准差,看看曲线的变化。
- 标准差决定了正态分布左右展开的幅度大小。
发现标准差变大,正态分布曲线变矮胖;同时标准差变小,正态分布曲线变高瘦。
平均不变,正态分布曲线的中心是不变,所以正态分布曲线的中心与标准差无关。
- 标准正态分布
所以如果平均和标准差的取值不同,曲线形状会有很多变化。
这当中平均为0,标准差为1的称为“标准正态分布”。
4.总结
・正态分布非常重要,原因是“不论总体是什么分布,只要从总体抽出的样本数足够多的时候,样本平均的分布符合正态分布。”
・正态分布的形态由平均和标准差决定。
・知道标准差后,范围内有多少观测数据也就知道了。
・用Excel的NORM.DIST函数可以描绘正态分布。
・平均为0,标准差为1的正态分布称为标准正态分布。