[统计学]什么是中心极限定理?一文搞懂中心极限定理
从前端的市场调研,到企业内部的数据分析,后端的品质管控等都有中心极限定理的影子。统计学号称宇宙最强学科,中心极限定理本身又是统计学中非常重要的一个定理。现在冬天里的一把火人工智能,简单说即是统计学+计算机,统计学指导计算机存储,演算数值。看不懂中心极限定理基本就告别自行车了。
中心极限定理是指给定一个任意分布的总体,每次从中随机抽取n个样本,一共抽m次,每组样本平均值分布接近正态分布。
什么是正态分布?请参考→[统计学]什么是正态分布?图解来说清楚
比如,一个6面骰子,一回合扔5次,进行10回合,结果如下。
| 次数\回数 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 | 九 | 十 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 3 | 2 | 2 | 2 | 2 | 3 | 2 | 3 | 3 | 3 |
| 2 | 2 | 3 | 3 | 4 | 5 | 4 | 5 | 5 | 6 | 5 |
| 3 | 2 | 5 | 2 | 4 | 1 | 2 | 2 | 4 | 1 | 4 |
| 4 | 4 | 4 | 3 | 2 | 2 | 1 | 4 | 5 | 3 | 3 |
| 5 | 5 | 4 | 5 | 2 | 5 | 3 | 2 | 3 | 5 | 2 |
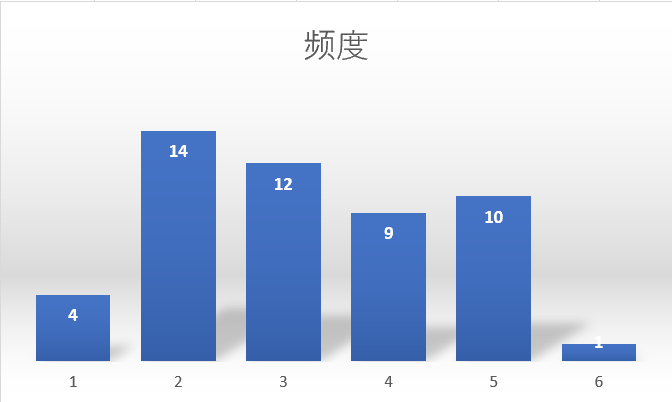
| 平均 | 3.2 | 3.6 | 2.8 | 2.8 | 3.0 | 2.6 | 3.0 | 4.0 | 3.6 | 3.4 |
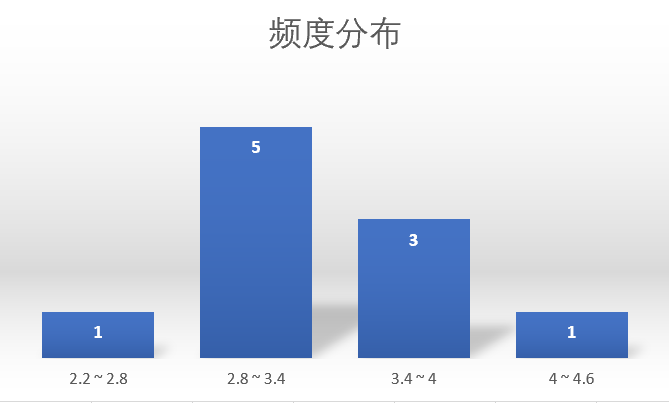
・6面骰子每个面摇到的概率都是1/6,所以摇到1~6出现的次数都应该几乎相同。因为取的样本数少,频率有些偏离概率,理想是1~6平齐。但是神奇的是,表中的平均用频次直方图画出来会发现看到了正态分布的影子!
→中心极限定理对总体的分布没有要求,可以是任意分布。
・上述栗子样本数量少,得到的正态分布图形有点奇怪 →下面我加大样本量,再进行说明。
用python处理数据和绘图都很方便,下面代码可以直接在jupyter notebook下运行。
import numpy as np
import matplotlib.pyplot as plt
dataset = np.random.randint(1, 7, 1000) # 随机生成1000个1~6的整数
fig = plt.figure() # 绘图相关,请点下面网址
ax = fig.add_subplot(1, 1, 1)
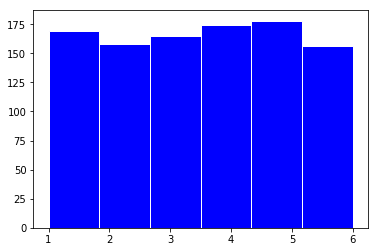
ax.hist(x=dataset, bins = 6,facecolor='blue',edgecolor='white', linewidth=1)关于matplotlib绘图想要学习更多↓ [Python]快速开始matplotlib matplotlib文档
可以看到,当样本数1000的时候,摇到1,2,3,4,5,6的次数就很接近了,各占了大约1000/6次。果然比上面的图看起来好多了。
sample = [] # 每次摇骰子的结果,[3, 4, 6, 4, ...]
samples = [] # 每次摇色子的结果的平均, [3.22, 3.64, 3.46, ... ]
for i in range(1,10001): # 摇骰子回数设为10000,注意[1,10001)前闭后开
sample = np.random.randint(1, 7, 50) # 随机生成50个1~6的整数,每回摇骰子次数设为50,
sample.mean() # 求每回50次的平均值
samples.append(sample.mean()) # 将每回的平均值放进samples里
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.hist(x=samples, bins = 9,facecolor='blue',edgecolor='white', linewidth=1)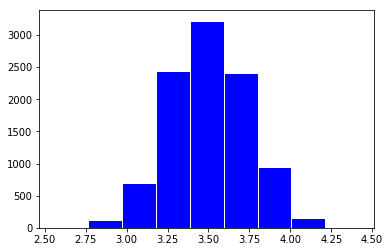
当回数增加到10000回,每回摇50次骰子的时候,每回摇骰子的平均值呈正态分布。看到这,你不得不禁感叹大自然的美妙!有兴趣你可以用任何分布的数据尝试,看看结果是否还符合正态分布。