[统计学]推论统计中的区间估计是什么？如何理解置信水平和置信区间？
目录
1.公司高层的依据充分吗?
2.全员的平均是多少？
3.点估计和无偏估计
4.估计还与什么有关？
5.区间估计，置信区间和置信水平
对工薪族来讲，最关心的就是工资。每天生活的开销都靠它，除了健康的身体之外也没别的资本，养老金也靠平日一点一点的积累。
我们这次就举个工资的栗子。
1.公司高层的依据充分吗?
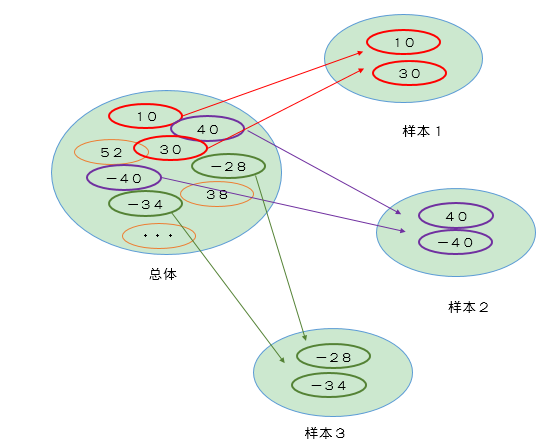
2名网络公司员工作为代表，跟公司高层开会交涉薪资条件，要求涨工资，不过进展并不顺利。会议中，高层问这两个人，你们去年工资存了多少？2人分别回答10万和30万。高层主张平均都存了20万了，这工资水平还叫低？不需要涨工资。这2个人一时没法反驳，像泄气的气球，郁闷地离开了会议室。问题是，这两个人真的就没法反驳了吗？
2.全员的平均是多少？
2人确实存下了钱，而且10万和30万一平均，确实也有20万。但是这20万是人数众多的员工中偶然选出来的，2人的平均值而已。说不定员工中有人不仅没存款，还是赤字。所有员工的平均的话，说不定接近0。只是碰巧这2个员工代表存了10万和30万而已。或者相反的，所有员工的平均的话，其实超过20万，碰巧这2人的平均为20万。
所以只从2个人存下钱的平均是20万，无法保证全员的平均是20万。
3.点估计和无偏估计
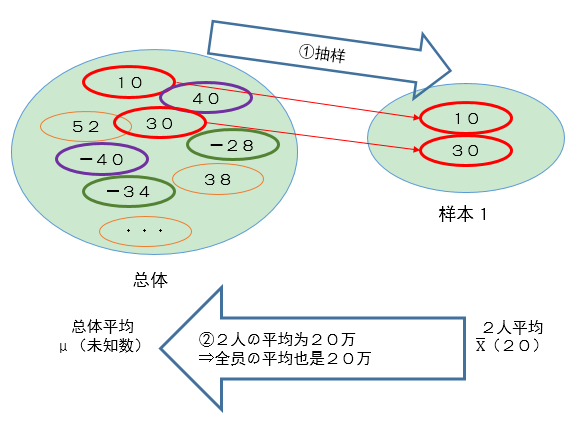
但是选出来的2人的存款额确实是10万和30万，这应该是估计全员平均存款额的重要线索。那如果根据从全员中随意挑选的2人的存款额是10万和30万，应该估计全员的平均存款额是多少才是合适的呢？最单纯的思路就是因为2人的平均值是20万，所以估计全员的平均值是20万。实际的平均值可能比20万高，也可能比20万低，但是没有理由来估计高一点，也没有理由来估计低一点，所以20万看起来是不高不低的公平的估计。
关于无偏估计学习更多→[统计学]什么是无偏估计？为何方差的无偏估计要/n-1?
但是各位不觉得这种点估计太没有技术含量了吗？因为偶然选出来的2人的平均为20万，所以估计全员的平均值也是20万。不过也没有别的思路，毕竟除了这点信息之外，好像也没有别的什么东西了。
4.估计还与什么有关？
留着这个问题，我们考虑以下这种情况。
假设2人的存款额不是10万和30万，2人分别是-60万和100万，平均还是20万。
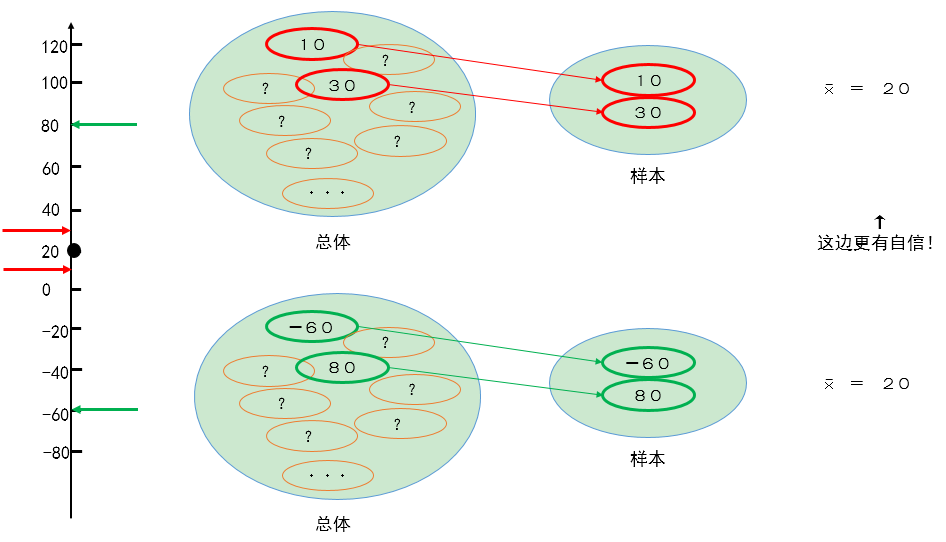
虽然这两种情况计算出来的平均都是20万，但是我们对结果的信心是不同的。10万和30万的话，都比较靠近20万，感觉全员平均是20万的可能性大一点，所以潜意识觉得平均应该不会是离20万很远的值。所以估计20万的话，还是比较有信心的。
但是如果是-60万和100万的话，2人的差异太大了，你猜不到其他人的存款的多少，所以说实话你也估计不出来平均是多少。因为就只有这两个值，只能把2人平均当做全员的平均，但是你肯定心虚。像这样数据越集中，你就越有信心，数据越离散，你就越没信心。
再设想一种情况，
现在是2人的平均20万得出全员平均是20万，所以没法消除这种可能：全员平均值其实离20万很远。如果选出100个人，得出的平均是20万的话，那全员的平均就在20万附近，不会离20万很远。所以数据越多，你的估计越有信心，数据越少，你对你所做出的估计就越没信心。
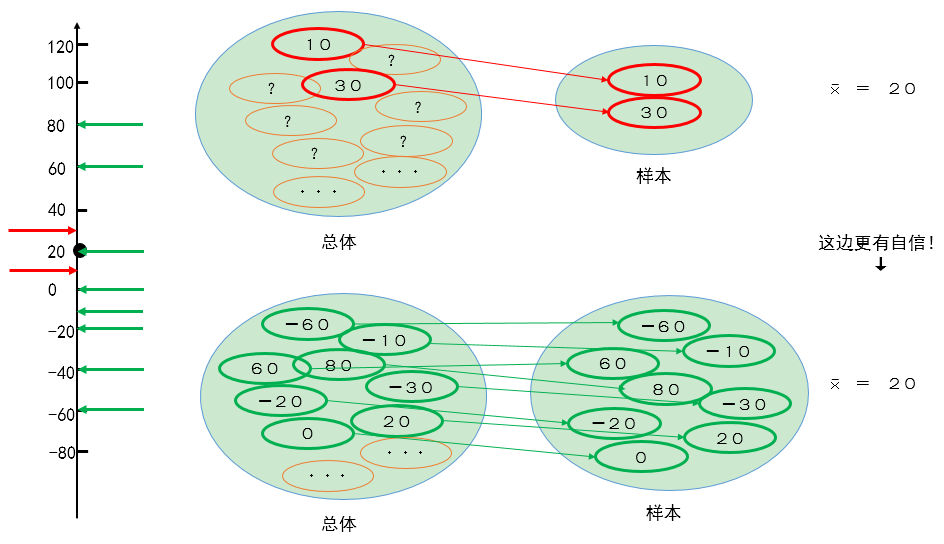
像这样，用全体员工(统计学中称为总体)中的样本来估计全体员工平均的时候，样本的离散程度越小，样本的数量越多，那估计的信心就越大。相反，标本的离散程度越大，样本的数量越少，估计时底气不足，信心就越小。我们把这种信心的程度换种说法。那怎样表达呢？
比如“全员的平均值在18万到22万的概率是90%”，或者“总体的平均值有95%的概率在15万~25万之间”，类似的都可以。这样表达的话，就很明了了，即概率越高的话，估计的自信越大，估计值存在的区间越小，估计的自信越大。
5.区间估计，置信区间和置信水平
这种估计是对估计值所存在的区间进行估计，所以称为区间估计。“总体的平均值有95%的概率在15万~25万之间”就是说“总体的平均值为95%的置信区间为15万~25万”。这里的95%称为置信水平，统计学用语。
很明显，区间估计比点估计要高级的多。将样本的数量及样本的离散程度也考虑进去，估计的信心也用数字进行了量化。
先把结果剧透一下。若代表着2人的存款为10万和30万，则全体的平均存款用区间估计进行计算的话，
50%的置信区间为10~30万
70%的置信区间为0~40万
90%的置信区间为-43万~83万
估计有90%的信心时，全员的平均是赤字的可能性也不小。所以开始的栗子中，可以说公司高层的主张是缺乏依据的。
那置信区间又该如何计算呢？
请参考→[统计学]一文看懂如何计算置信区间